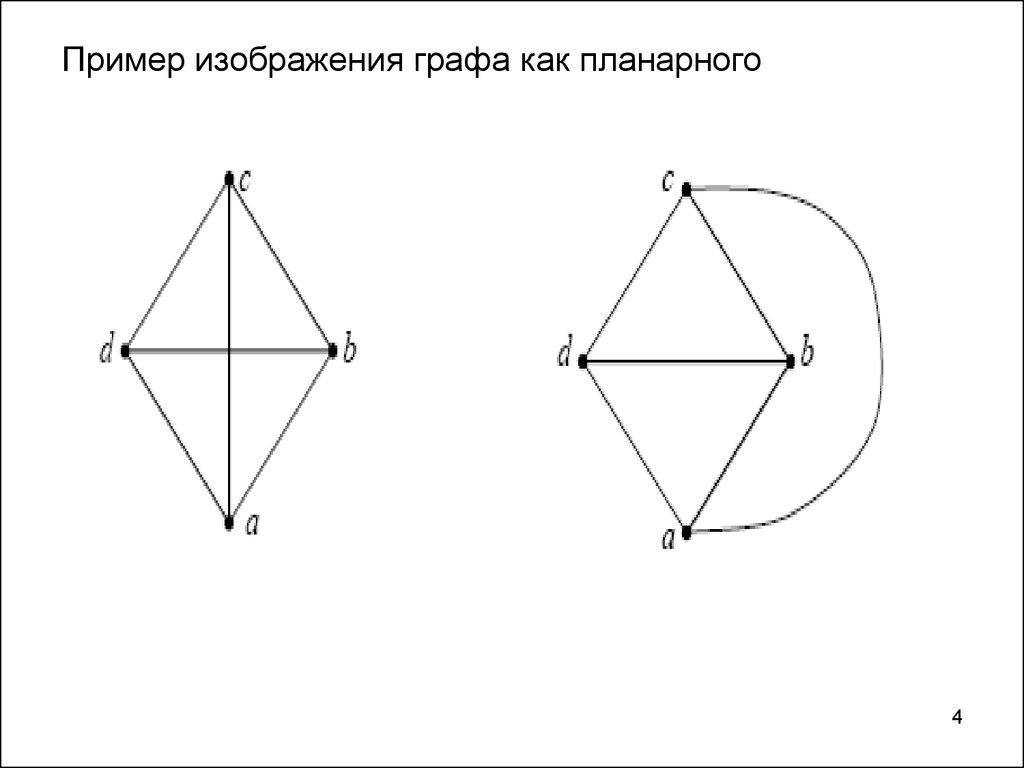
Планарные графы и раскраска

В теории топологических графов , 1-планарный граф - это граф, который можно нарисовать в евклидовой плоскости таким образом, чтобы каждое ребро имело не более одной точки пересечения, где он пересекает одну дополнительную кромку. Если 1-планарный граф, одно из наиболее естественных обобщений планарных графов , нарисован таким образом, рисунок называется 1-плоскостным графом или 1-планарным. Позже было показано, что точное количество цветов, необходимых для раскраски этих графиков, в худшем случае, равно шести.

Графы. Раскраска графов. (Тема 3)

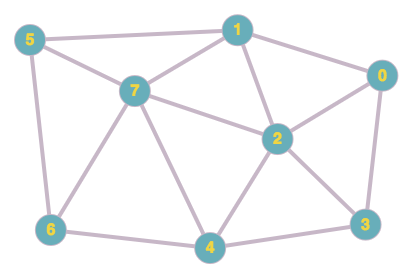
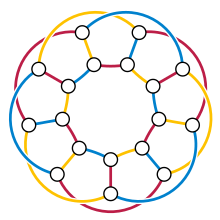
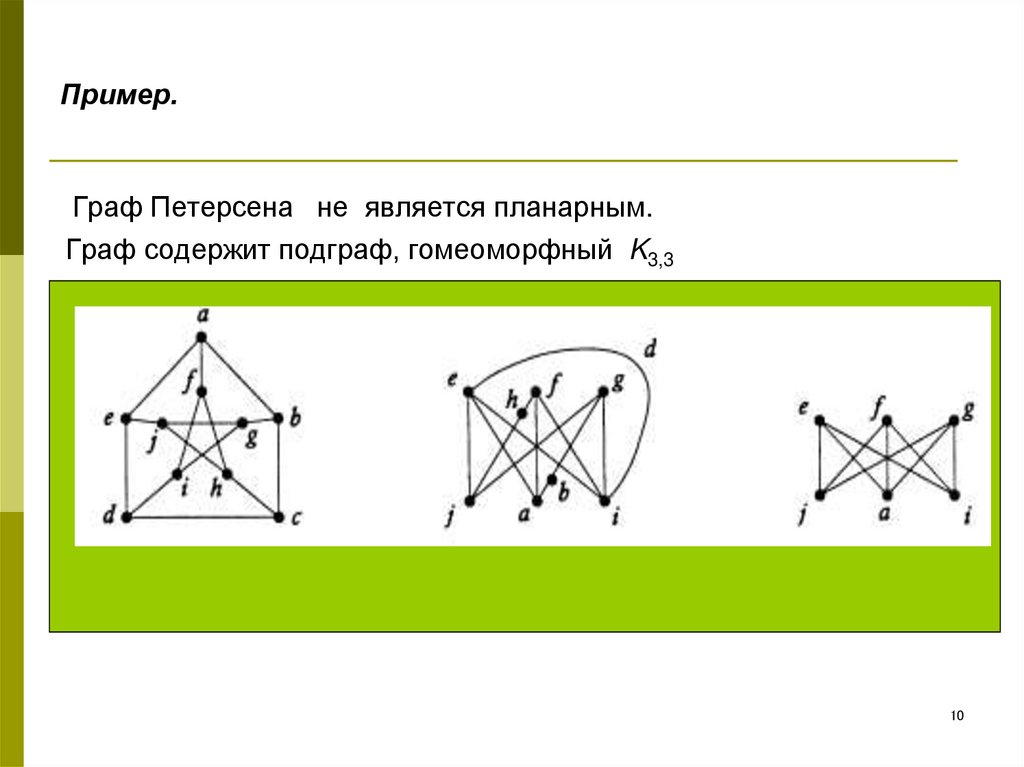
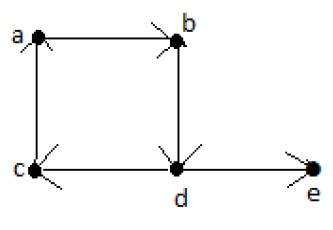
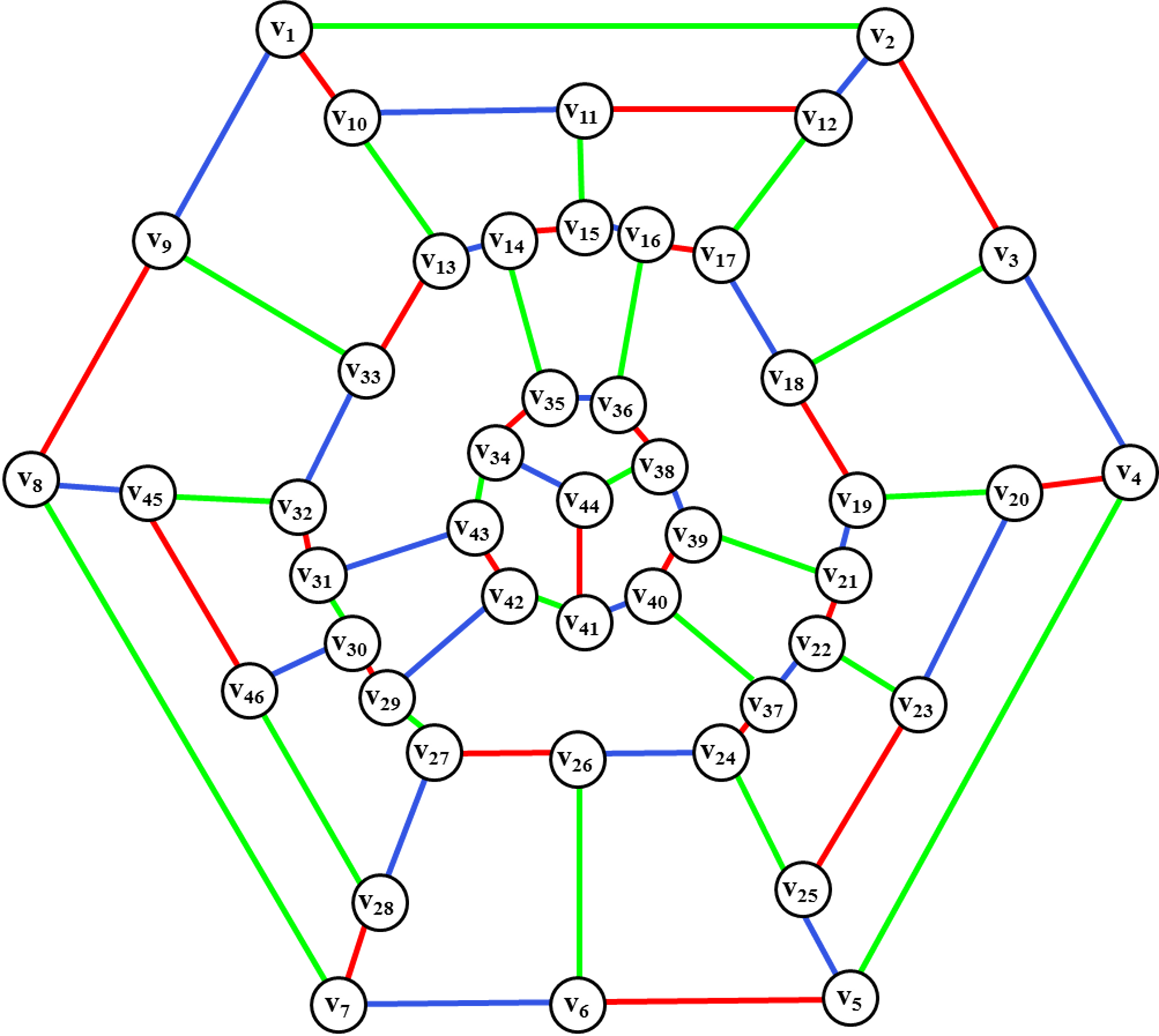
В теории графов , край окраски из графика является присвоение «цветов» к краям графика , так что никакие два ребра инцидента не имеют такой же цвет. Например, на рисунке справа показана окраска ребер графа красным, синим и зеленым цветами. Раскраска ребер - это один из нескольких различных типов раскраски графов. Задача раскраски ребер спрашивает, можно ли раскрасить ребра данного графа, используя не более k различных цветов, для данного значения k или наименьшего возможного количества цветов. Минимальное необходимое количество цветов для ребер данного графа называется хроматическим индексом. Например, края графа на иллюстрации могут быть окрашены в три цвета, но не могут быть окрашены в два цвета, поэтому показанный граф имеет хроматический индекс три.

Раскраски и укладки графов. Alex Dainiak researcher. Раскраски и укладки графов 1 of Download Now Download to read offline. Recommended Теорема о 5 красках.

• Алгебра приходит на помощь
• В этой небольшой заметке я хочу показать, как с помощью алгебры можно решать классическую задачу о раскраске вершин графа. Об этом сюжете я узнал из книги W.
• Курсовая работа по дисциплине "Теория графов", Омский государственный технический университет, преподаватель Финк Т. Приведена теория, программа, алгоритм, практическое приложение задачи:.
• Раскраска графа — теоретико-графовая конструкция, частный случай разметки графа.

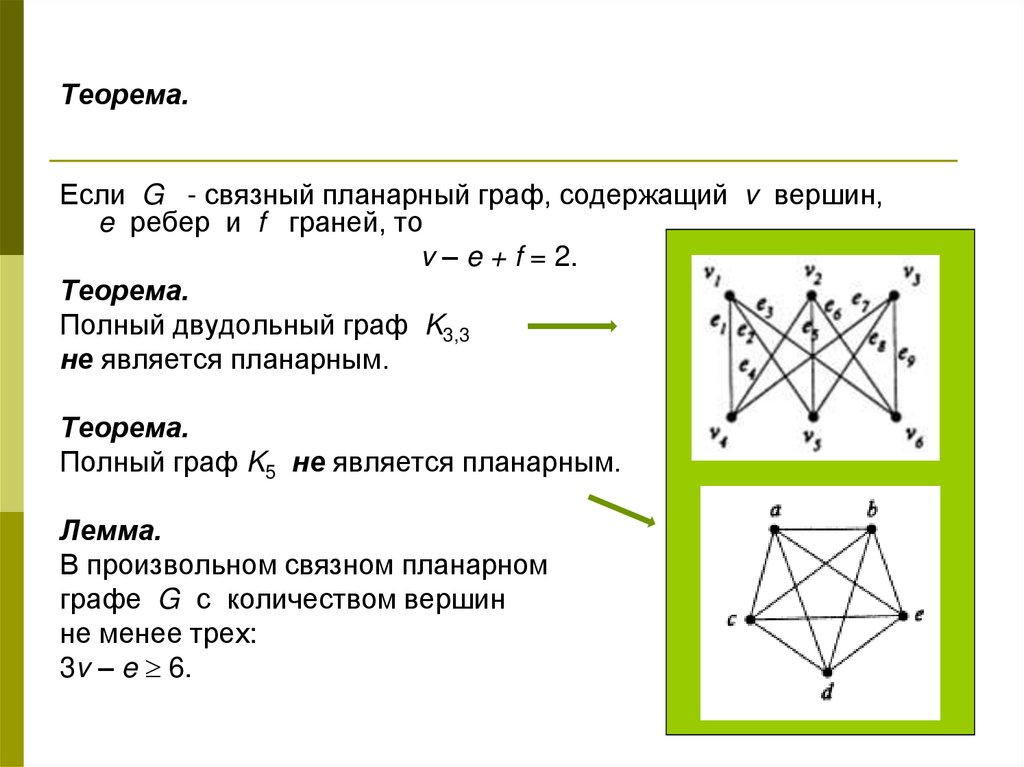
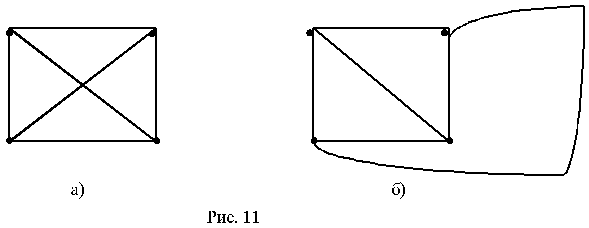
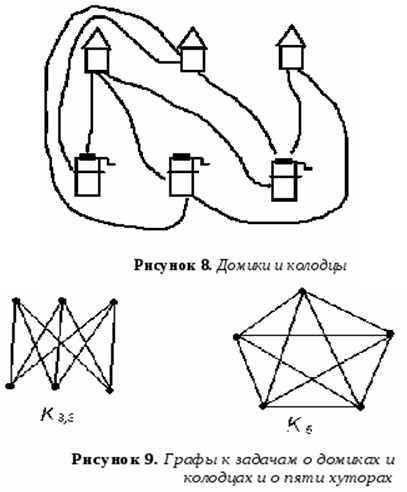
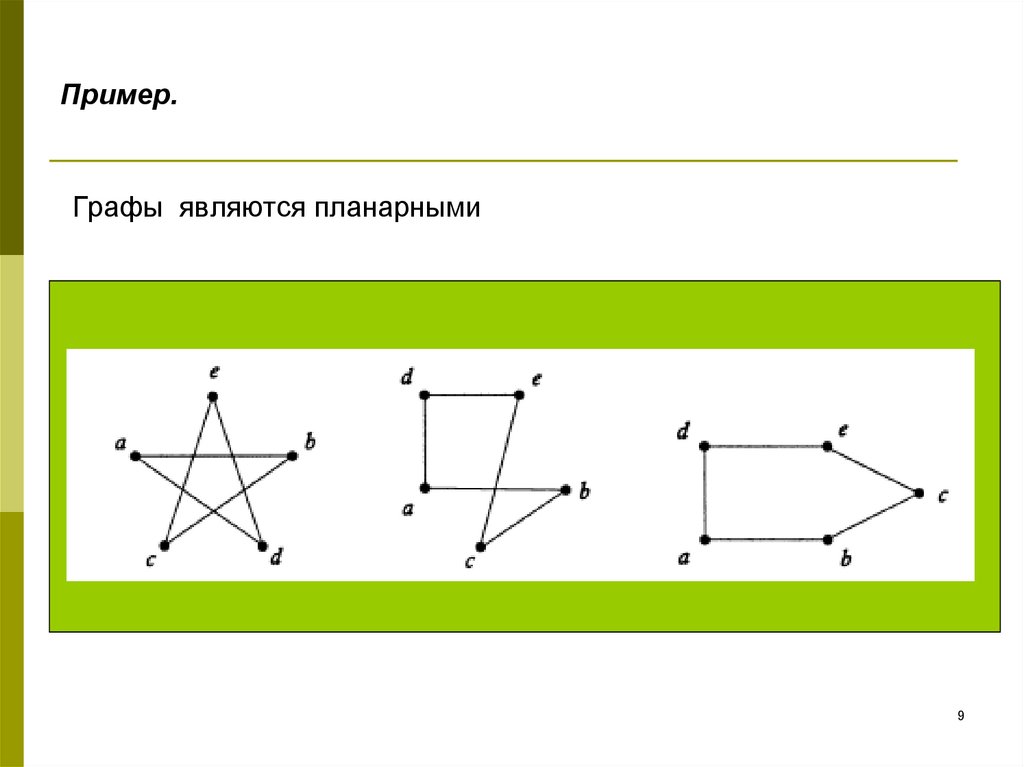
Рассматриваем раскраски планарных графов и другие темы, связанные с раскрасками. Доказываем теорему Томассена о том, что списочное хроматическое число любого планарного графа не превышает пяти. Доказываем теорему Эрдёша о том, что существуют графы с большим хроматическим числом и одновременно большим обхватом. Рассматриваем совершенные графы и доказываем слабую гипотезу Бержа. Основы теории графов раскраски планарных графов, совершенные графы. Alex Dainiak researcher.

Похожие статьи

• Лиса в раскраске
• Персонажи сказок раскраски
• Распечатать раскраску кота саймона
• Распечатать раскраску солдатов